For example for positive integers p and q and non-square n it is true that if p 2 nq 2 1 then p q is a convergent of the regular continued fraction for n. N are irrational.
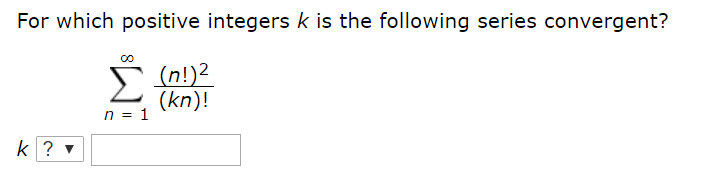
Solved For Which Positive Integers K Is The Following Series Chegg Com
Then as in the previous paragraph the axioms.
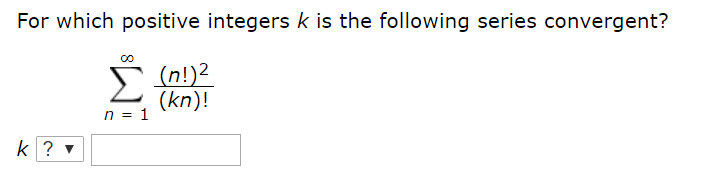
. State whether each of the following series converges absolutely. N 1 a n. F n a n f n a n for all integers n 1.
Let S N S N be the Nth partial sum of n 1 a n. Thus kqk q for every positive rational number. Suppose n 1 a n n 1 a n is a convergent series with positive terms.
For example at least one of ζ5 ζ7 ζ9 or ζ11 is irrational. There are also results on the irrationality of values of the Riemann zeta function at the elements of certain subsets of the positive odd integers. Kbk 1 for all positive integers b.
Then using the algebraic limit properties of convergent series. Is another positive integer then knkkmnk kmk kmnk kmkknk m n mn. Finally if qis a positive rational number then k qk k 1kkqk q j qj so kxk jxj holds for all x2Q including 0.
The converse holds if the period of the regular continued fraction for n is 1 and in general the period describes which convergents give solutions to Pells equation. Series 1 shown in Equation 511 is a geometric series. It is known that ζ3 is irrational Apérys theorem and that infinitely many of the numbers ζ2n 1.
Where b n 0 b n 0 for all positive integers n. Suppose there exists a function f f satisfying the following three conditions. F f is continuous f f is decreasing and.

For Which Positive Integers Of K Is Series Convergent N Kn Youtube
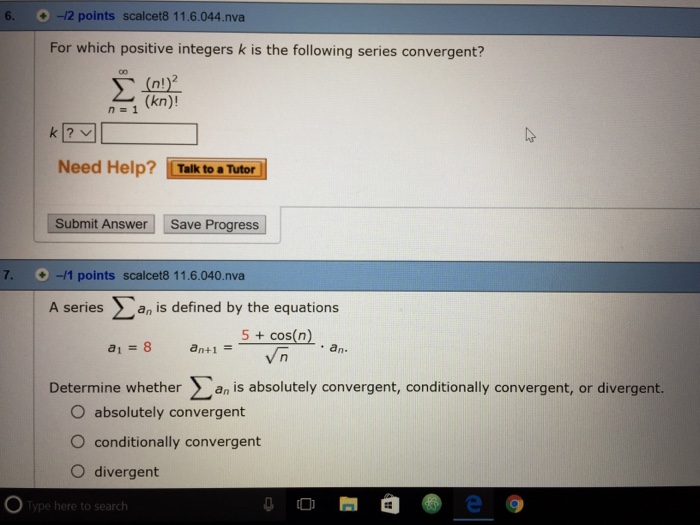
Solved For Which Positive Integers K Is The Following Series Chegg Com
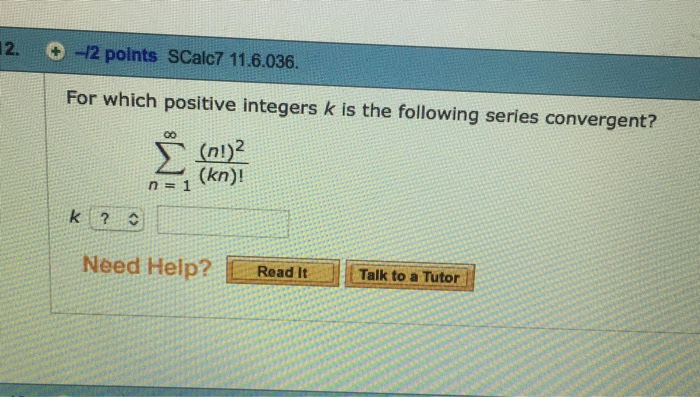
Solved For Which Positive Integers K Is The Following Series Chegg Com
0 Comments